[알고리즘] 분할 정복 거듭 제곱 계산 - 코딩밥상

거듭 제곱(Exponentiation) 계산

거듭 제곱은 컴퓨팅에서 자주 사용되는 연산 중 하나입니다. 하지만 일반 산술 연산과 달리 의외로 수행시간이 오래 걸리는데, 이 문제를 분할 정복으로 해결할 수 있습니다.

 

먼저 거듭 제곱의 계산법을 살펴보면

C^n 을 계산 하려면 C*C*C*...*C 와 같이 C자신을 n번 곱해야 합니다.

지수의 크기만큼 곱셈을 수행하므로 O(n)의 수행 시간을 소요하는 것입니다.

long Poewr(int Base, int Exponent){
    int Result = 1;
    
    for(int i=0; i<Exponent; i++) Result *= Base;
    
    return Result;
}

 

이보다 더 좋은 성능으로 개선할 방법으로 중학생때 배웠던 '지수 법칙'을 활용할 수 있습니다.

예를들어 C^8 = C*C*C*C*C*C*C*C과 같이 정의되지만,

C^8 = C^4 * C^4 = (C^4)^2 = ((C^2)^2)^2 와 같이 C^2를 구한 후 세 번의 곱셈만을 수행하여 결과를 얻을 수 있습니다.

하지만 홀수의 경우 위와 같이 나누어 떨어지지 않으므로 나누어 생각해 줘야겠네요.

n이 홀수일 경우에는 C^n = C^(n-1)/2 * C^(n-1)/2 * C 와 같이 정리 할 수 있습니다.

 

식으로 정리하면,

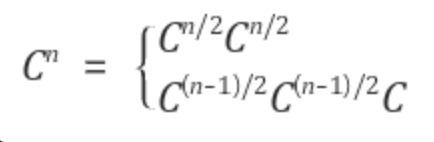
첫 번째는 n이 짝수일 때, 두 번째는 n이 홀수일 때 입니다.

 

이렇게 지수를 두개씩 쪼개면서 계산을 해나가기에 분할 정복이라고 할 수 있습니다. 수행 시간 또한 O(n)에서 O(logn)으로 비약적으로 향상되었네요.

---

분할 정복 거듭 제곱 계산 구현

long Power(int Base, int Exponent){
    if(Exponent == 1) return Base;
    else if (Base == 0) return 1;
    
    if(Exponent%2 == 0){
        long NewBase = Power(Base, Exponent/2);
        return NewBase * NewBase;
    }
    else{
        long NewBase = Power(Base, (Exponent-1)/2);
        return NewBase * NewBase * Base;
    }
}