허프만 코딩이란?
음악 저장 파일 포맷인 mp3와 이미지 저장 파일 포맷인 JPEG의 공통점은 바로 이 허프만 코딩을 이용하는 압축 데이터 포맷이라는 점입니다. 즉 이 알고리즘은 성능이 가장 우수한 압축 알고리즘 중 하나입니다.
고정 길이 코드와 접두어 코드
허프만 코딩을 이해하려면 먼저 몇가지 기본 지식을 알아야 합니다. 우선 고정 길이 코드(Fixed Length Code)는 말 그대로 모든 코드의 길이가 똑같은 값을 갖는 코드 체계를 말합니다. 코딩을 하면서 자주 사용하는 ASCII가 대표적인 예 입니다.
고정 길이 코드가 연산의 편의를 위한 것이라면 가변 길이 코드(Variable Length Code)는 저장 공간 절약을 위해 사용됩니다. 그만큼 데이터 처리는 상당히 번거롭겠네요.
접두어 코드(Prefix Code)는 가변 길이 코드의 한 종류입니다. '접두어'는 다른 낱말 앞에 위치해서 새로운 낱말을 만드는 역할을 합니다. 접두어 코드는 코드 집합의 어느 코드도 다른 코드의 접두어가 되지 않는 코드를 말합니다. 때문에 '무접두어 코드'라고도 불리고 이 명칭이 의미를 더 명확하게 알려주는것 같네요.
다시 돌아와서 예를 들어 {"0", "1", "01", "010"}은 접두어 코드가 아닙니다. 반면에 {"00", "010", "100", "101"}은 어느 코드도 다른 코드의 접두어가 되지 않기 때문에 접두어 코드라고 할 수 있습니다.
ASCII와 같이 고정 길이 코드로 이루어진 데이터를 접두어 코드로 변환할 수 있는 메커니즘이 있다면 데이터를 압축 할 수 있습니다. 그와 반대로 동작하는 메커니즘은 압축된 데이터를 원본으로 압축 해제할 수 있고요. 허프만 코딩은 이런 아이디어에 근거를 두고 있습니다.
허프만 트리 구축
허프만 코딩 알고리즘은 두 가지 키워드가 있습니다. '기호의 빈도'와 '이진 트리'입니다.
'기호의 빈도'는 한 기호가 데이터 안에서 차지하는 비율을 말합니다. 이는 길이가 짧은 접두어 코드를 빈도가 높은 기호에 부여하기 위해 사용됩니다. 빈도가 높은 기호에 작은 접두어를 부여하면 그만큼 저장 공간을 아낄 수 있기 때문입니다. 즉 압축율이 높아집니다.
'이진 트리'는 접두어 코드를 표현하기 위해 사용됩니다. 트리의 노드에서 왼쪽 자식 노드는 0, 오른쪽 자식 노드는 1을 나타냅니다. 이 트리에서 모든 기호는 잎 노드에만 기록되어 있으며 뿌리 노드에서부터 잎 노드까지 이르는 경로가 기호의 접두어 코드가 됩니다.
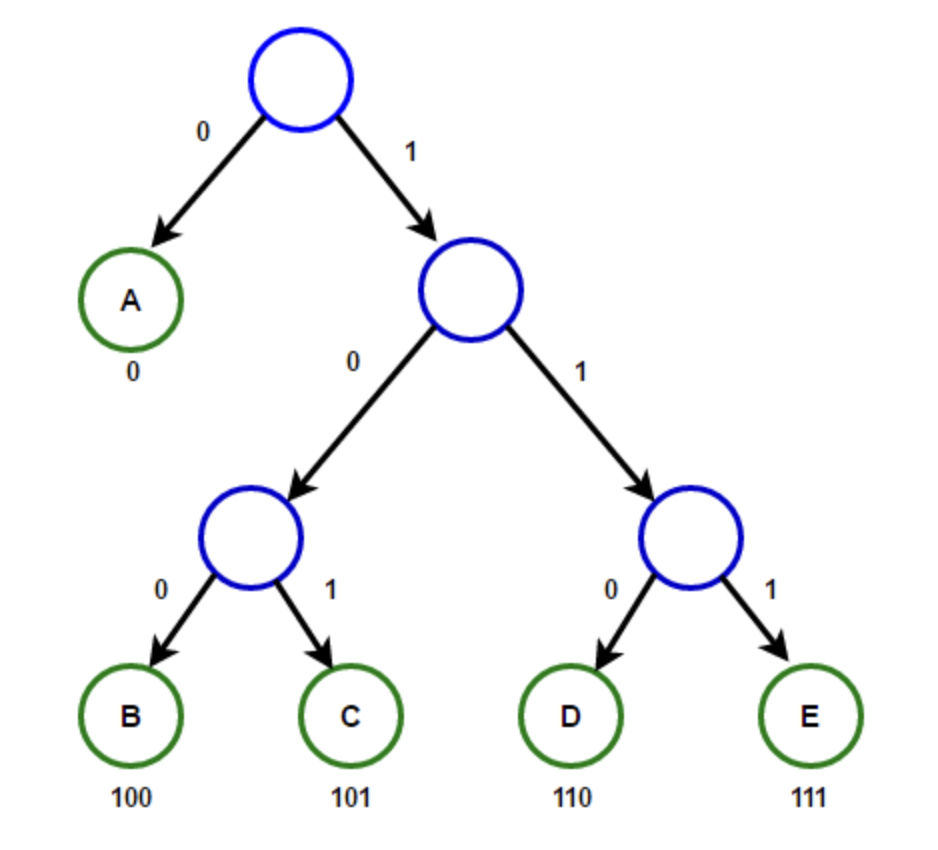
이러한 방식으로 접두어 코드를 표현하는 이진 트리를 허프만 트리(Huffman Tree)라고 합니다.
앞에서 정리한 기호의 빈도와 이진트리를 활용하여 빈도가 높은 기호일수록 경로를 짧게, 빈도가 낮은 기호일수록 경로를 길게 가져가면 압축률이 높아지겠네요. 그렇다면 어떻게 해야 빈도수가 높은 기호부터 경로가 짧은 노드로 들어갈 수 있도록 만들까요? 그리고 이것이 왜 그리디 알고리즘과 연관이 있을까요?
지금부터 그리디 알고리즘의 3단계를 적용해 문제를 풀어나가겠습니다.
'해 선택' : 선택 기준은 현 시점에서 빈도가 가장 작은 노드 2개 입니다. 노드를 선택한 후 두 노드 위에 부모 노드를 새로 만들어 각각 왼쪽과 오른쪽에 연결시킵니다.
'실행 가능성 검사' : 노드를 선택한 후 두 노드 위에 부모 노드를 새로 만들어 각각 왼쪽과 오른쪽에 연결시킵니다. 이때 부모 노드의 빈도는 자식 노드 빈도의 합이 됩니다. 기호를 가진 노드는 잎 노드여야 합니다.
'해 검사' : 허프만 트리가 완성되어야 합니다. 그렇지 않다면 위 단계들을 반복합니다.
데이터 압축과 해제
-압축
허프만 트리는 압축을 위해 만들어졌습니다. 문자열의 각 요소를 차례대로 읽으면서 허프만 트리가 나타내는 해당 문자의 접두어 코드로 변환하면 압축이 됩니다.
여기서 궁금증은 접두어 코드를 알아내기 위해 매번 허프만 트리를 순회해야될까요? 이 문제를 해결하려면 별도의 테이블을 만들어 접두어 코드를 저장하는 방법이 있겠네요. 즉 공간을 팔아서 성능을 얻는 것입니다.
-해제
허프만 코딩은 압축뿐 아니라 압축을 풀어내는 방법도 제공합니다. 당연히 그래야 사용할 수 있겠죠.
- 허프만 트리와 압축 해제된 데이터가 담길 버퍼를 준비합니다. 여기서 허프만 트리의 뿌리 노드로부터 시작해서 잎 노드까지 순회합니다.
- 압축 데이터에 아직 읽지 않은 부분이 남아있다면 데이터를 한 비트 읽습니다.
- 읽어낸 비트가 0이면 현재 노드의 왼쪽 자식 노드, 1이면 오른쪽 자식 노드로 이동합니다. 현재 노드가 잎 노드면 버퍼에 저장된 기호를 추가하고 다시 뿌리 노드로 이동합니다.
즉 비트를 읽을 때마다 잎 노드를 만나기 전까지 허프만 트리의 왼쪽과 오른쪽으로 노드를 순회하고, 잎 노드를 만나면 버퍼에 추가하고 뿌리 노드로 이동해 처음부터 과정을 반복합니다.
'알고리즘 > 탐욕 알고리즘(Greedy)' 카테고리의 다른 글
| [알고리즘] 탐욕(Greedy) 알고리즘 - 코딩밥상 (1) | 2023.01.29 |
|---|