[Java] 실수형 변수(float, double) - 코딩밥상
실수형 변수 float, double
실수형의 표현 범위
실수형은 말그대로 실수를 저장하기 위한 변수 타입으로 float와 double 두 가지가 있으며 각 타입의 변수에 저장할 수 있는 값의 범위는 다음 표와 같다.

즉 실수형은 소수점도 표현해야 하므로 '얼마나 큰 값을 표현할 수 있는가'뿐만 아니라 '얼마나 0에 가깝게 표현할 수 있는가'도 중요한 요소이다.
여기서 생기는 궁금점이 '4byte의 정수로는 약 +-2*10^9 범위의 값밖에 표현 가능한데 어떻게 같은 4byte로 +-3.4*10^34와 같은 큰 값을 표현할 수 있을까?' 이다.
이에 대한 답은 값을 저장하는 방식이 다르기 때문이다.

일반적인 방법인 고정 소수점 방식을 사용하면 '부호'와 '값(정수 + 소수)' 만으로 직관적으로 표현하지만,
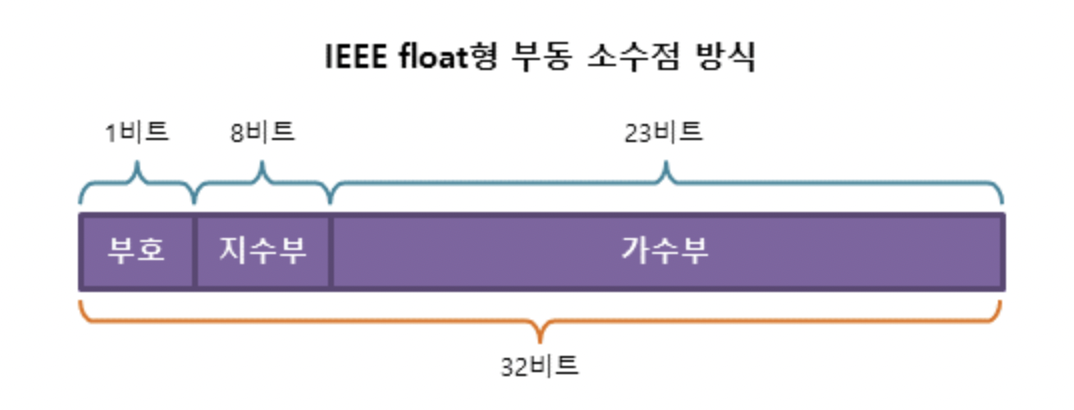
부동 소수점 방식은 '부호(S)' '지수(E)' '가수(M)' 세 부분으로 표현한다. 이는 2의 제곱을 곱한 형태로 표현되는데,
+-M * 2^E 형태로 저장되는 것이다.
때문에 고정 소수점 방식보다 훨씬 큰 범위를 저장 할 수 있게 되는 것입니다.
그러나 정수형과 달리 실수형은 오차가 발생할 수 있다는 단점이 있다. 맨 위에있는 표를 보면 float타입은 정밀도가 7, double 타입은 정밀도가 약 2배인 15인 것을 알 수 있다.
정밀도는 'a * 10^n' (1<=a<10)의 형태로 표현된 10진수 값을 오차없이 저장할 수 있다는 뜻이다. 따라서 float 타입은 7자리의 10진수, double 타입은 15자리의 10진수를 오차없이 표현 할 수 있는 것이다.
실수형의 저장 방식
| 기호 | 의미 | 설명 |
| S | 부호(Sign bit) | 0이면 양수, 1이면 음수 |
| E | 지수(Exponent) | 부호있는 정수. 지수의 범위는 -127 ~ 128(float), -1023 ~ 1024(double) |
| M | 가수(Mantissa) | 실제값을 저장하는 부분. 10진수로 7자리(float), 15자리(double)의 정밀도로 저장 가능 |


1. 부호(Sign bit)
부호를 저장하는 부분으로 값이 0이면 양수, 1이면 음수를 의미합니다. 따라서 1bit로 표현한다.
주의할 점은 정수형과 달리 '2의 보수법'을 사용하지 않기 때문에 양의 실수를 음의 실수로 바꾸려면 그저 부호비트만 반대로 변경하면 된다.
2.지수(Exponent)
지수를 저장하는 부분으로 float의 경우 8bit의 저장공간으로 256개의 값을 저장하는데 부호가 존재하므로 '-127 ~ +128'의 값을 저장한다. 이 중 -127과 128은 무한 값이나 NaN 값을 저장하기에 실제로 사용 가능한 지수의 범위는 '-126 ~ +127'이다.
따라서 float 타입으로 표현할 수 있는 최대값은 2^127이고, 10진수로 약 10^38인 것이다.
그러나 float 타입으로 표현할 수 있는 최소값은 가수의 마지막 자리가 2^-23이므로 지수의 최소값보다 그만큼 더 작은 값인 약 10^-45이다.
double타입의 최대값과 최소값도 같은 방법으로 정해진다.
3.가수(Mantissa)
실제 값인 가수를 저장하는 부분으로 float의 경우, 2진수 23자리를 저장할 수 있습니다. 2진수 23자리로는 약 7자리의 10진수를 저장할 수 있는데, 이것이 바로 float의 정밀도가 되는 것이다.
double의 경우 가수를 저장할 수 있는 공간이 52자리로 float보다 약 2배 이고, 따라서 정밀도 또한 약 2배를 갖는 것이다.
부동소수점의 오차
실수 중에는 무한소수가 존재하므로, 정수와 달리 실수를 저장할 때는 오차가 발생할 수 있다. 게다가 10진수가 아닌 2진수로 저장하기 때문에 10진수로는 유한소수이더라도, 2진수로 변환하면 무한소수가 되는 경우도 있다. 2진수로는 10진 소수를 정확히 표현하기 어렵기 때문이다.
이때 가수를 저장할 수 있는 자리수가 한정되어 있으므로 저장되지 못하고 버려지는 값들이 있으면 오차가 발생하게 된다.
실수타입(float)을 저장하는 예를 통해 정리해보면,
1. 변환하고자 하는 숫자에 절댓값 붙이고 2진수로 변환
: 6.25 [10] → 110.01 [2]
2. 1.xxxx 형식으로 바꾸기(=1.M × 2^E)
: 110.01 [2] = 1.1001 × 2^2
3. E에 기저수를 더한 뒤, 2진법으로 변환 [float 기저수 127, double 기저수 1023]
: (float 기준) 129 [10] → 10000001 [2]
4. 부호 'S' + 2진법으로 변환된 지수 'E'+가수 'M'
: (S)0 (E)10000001 (M)10010000000000000000000
위 예의 경우 적절한 값(6.25)을 저장했기 때문에 오차가 없지만 만약 저장하고자 하는 소수의 자릿수가 오차 범위를 넘어가면 가수(M)부분이 길어지고 float의 경우 23bit(2^-23 약 10^-7), double의 경우 52bit(2^-52 약 10^-15) 범위를 넘어가면 잘려나가기때문에 정밀도가 각각 7, 15가 되는것이다.
알쓸정보
-실수형에서도 변수의 값이 표현범위의 최대값을 벗어나면 '오버플로우'가 발생하는데, 정수형과 달리 실수형에서는 '무한대(infinity)'가 됩니다. 또한 정수형에는 없는 '언더플로우'가 있는데, 실수형으로 표현할 수 없는 범위를 벗어난 작은 값에 대해서 발생합니다. 이 때 변수의 값은 0이 됩니다.
-위에서 정리한바와 같이 float의 표현 범위는 약 1.4 * 10(-45승) ~ 3.4 * 10(38승)으로 거의 만날 일이 없는 크고 작은 값들입니다. double의 범위는 이 보다 넓은 범위입니다.
하지만 정밀도측면에서 보면 float은 7자리의 값만 정확하게 표현할 수 있고 double은 약 2배인 15자리의 값까지 정확히 표현할 수 있기 때문에 실수형 값을 저장할 때 float타입이 아닌 double타입의 변수를 사용하는 경우는 대부분 저장하려는 '값의 범위'때문이 아니라 '보다 높은 정밀도'가 필요해서입니다.
즉 연산 속도 향상이나 메모리를 절약하려면 float을, 높은 정밀도를 필요로 한다면 double을 선택합니다.